A state department of education, as a question on the public-release form of a statewide standardized test, released a question to the public in which eighth-grade students have to determine how many bracelets a girl can make, given that each bracelet requires 1/8 yard of string and she has 3/4 of a yard of string total.
There are several approaches to solving this problem. The easiest approach is simple arithmetic. If we have so much of something and we need to use a certain portion of that each time to make something, we need to know how many of those portions are in the total that we start with.
Let’s suppose you’re in charge of bringing the water for a charity run or marathon at your school. You have a total of 100 liters of water, and you know from the person who was in charge of the water last year that each runner will drink exactly two liters of water during the marathon. Given that information, how many runners can you have? 50, right?
Now, how did you get that answer of 50? Well, you simply divided the total amount of water you have by the amount used by each runner. 100 divided by 2 is 50, and hence your answer.
This problem really isn’t much different, except the amounts are in terms of fractions. The mathematical process you use to find the answer is exactly the same (except that making bracelets may be more fun for some people than running a marathon … not for me, though).
And that same mathematical process involves taking the total that you have (3/4 of a yard) and dividing it by the amount you need for each bracelet (1/8 of a yard). When we divide one fraction by a second fraction, remember, we have to change to multiplication and invert the second fraction:
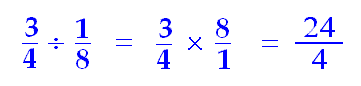
Our answer (24/4) is equivalent to 6, and that is how many bracelets the girl can make with the amount of string she has.
If you would like additional problems to help you master this skill, go to our online card catalog at VoxLearn.org, select one of the math collections, and enter the search terms “divide fraction models”.













A marathon is exactly 26 7/32 miles.
A 10K run is approximately 6 2/10 miles.
Given this approximation, how many 10K runs have you done after you complete an entire marathon?
First, convert everything to improper fractions, and then divide the marathon into pieces, each of which constitutes a 10K run:
And in conclusion, a marathon is about 4 and a quarter 10K runs. You have run more than four 10Ks if you complete a marathon.
As I noted in the original post, you have a few choices in terms of the procedure you use to solve this problem.
Another one that comes to mind is that you might use your number sense and realize that there are two eighths in one fourth. And then, the girl in the bracelet-and-string problem has three of those fourths worth of string.
If she can get two bracelets out of every one-fourth yard of string, and she has three-fourths of a yard of string, she can get 2 × 3 = 6 bracelets out of the total amount of string she has.
Illinois Alignment
Grade Level 8
Illinois Learning Standard 6.B.3a (middle school) Solve practical computation problems involving (whole numbers, integers and) rational numbers.
Illinois Assessment Framework 6.8.09 (8th grade) Solve problems and number sentences involving (addition, subtraction, multiplication, and) division using rational numbers (, powers, and roots).